6. Intuitive Limits and Continuity

b. Intuitive Definitions

1. Left and Right Limits

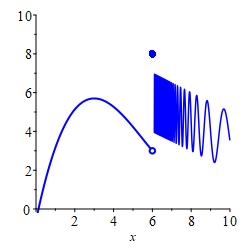
Given a function, \(f(x)\), and a point, \(x=a\), there are \(3\) quantities which describe the behavior of \(f(x)\) at and near \(x=a\).


The value of the function is \(f(a)\).
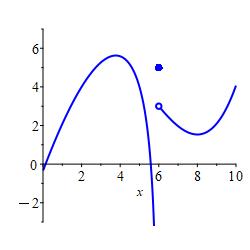
In the plot, \(a=6\) and \(f(6)=8\) which is the solid circle at \((6,8)\).

The limit of the function, \(f(x)\), as \(x\) approaches \(a\) from the left is the number, \(L\), that \(f(x)\) approaches as \(x\) approaches \(a\) from the left. We write: \[ \lim_{x\to a^-}f(x)=L \] In the plot, \(a=6\) and \(L=5\) which is the open circle at \((6,5)\).

The limit of the function, \(f(x)\), as \(x\) approaches \(a\) from the right is the number, \(L\), that \(f(x)\) approaches as \(x\) approaches \(a\) from the right. We write: \[ \lim_{x\to a^+}f(x)=L \] In the plot, \(a=6\) and \(L=3\) which is the open circle at \((6,3)\).

def_LR_lim.jpg
For this function: \[\begin{aligned} \lim_{x\to 6^-}f(x)=5 & \qquad \lim_{x\to 6^+}f(x)=3 \\ \text{and} \quad & \quad f(6)=8 \end{aligned}\]

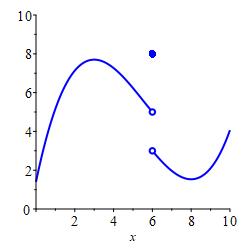
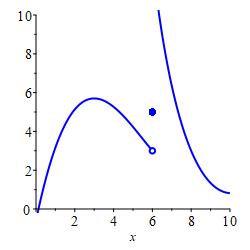
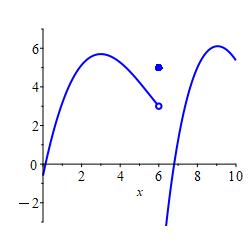
All three of these numbers may or may not exist and, in general, they can all be different. In the plot above, all three numbers exist and are all different. In the plot on the left below, the function value exists but is different from the limits from the left and right which happen to be equal. In the plot on the right below, the limits from the left and right exist and happen to be equal while the function value does not even exist. This has no effect on the limit. The limits are only concerned with what values \(f(x)\) approaches as \(x\) nears \(a\).

def_LR_val_exists
The limits exist but the function value is different.
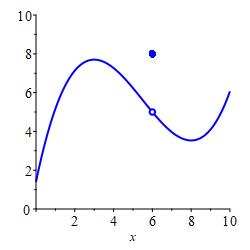
In this case, \(\displaystyle \lim_{x\to 6^-}f(x) =\lim_{x\to 6^+}f(x) =5\)
def_LR_val_dne
The limits exist but the function value is undefined.
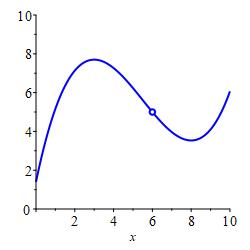
Again, \(\displaystyle \lim_{x\to 6^-}f(x) =\lim_{x\to 6^+}f(x) =5\)


If a limit exists, we say it converges.
If a limit does not exist, we say it diverges.

This is an intuitive preliminary definition. The actual precise definition appears on a later page. However, the precise definition is not essential for this course. Everything can be based on the intuitive definition.

When Limits Do Not Exist

The six plots below show six situations in which a limit from the left or right does not exist.

def_L_inf
\(\displaystyle \lim_{x\to 6^-}f(x)=\infty\)
def_L_minf
\(\displaystyle \lim_{x\to 6^-}f(x)=-\infty\)
def_L_osc
\(f(x)\) is oscillatory divergent
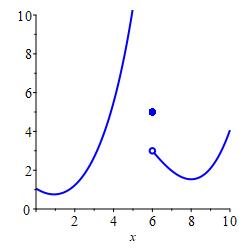
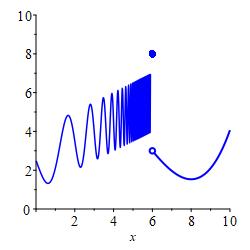
from the left.
def_R_inf
\(\displaystyle \lim_{x\to 6^+}f(x)=\infty\)
def_R_minf
\(\displaystyle \lim_{x\to 6^+}f(x)=-\infty\)
def_R_osc
\(f(x)\) is oscillatory divergent
from the right.


We say a left or right limit is positive infinity if \(f(x)\) gets arbitrarily large and positive as \(x\) approaches \(a\) from the left or right (resp.). We also say \(f(x)\) diverges to \(\infty\) on the left or right and write: \[ \lim_{x\to a^-}f(x)=\infty \qquad \lim_{x\to a^+}f(x)=\infty \qquad \text{resp.} \]

We say a left or right limit is negative infinity if \(f(x)\) gets arbitrarily large and negative as \(x\) approaches \(a\) from the left or right (resp.). We also say \(f(x)\) diverges to \(-\infty\) on the left or right and write: \[ \lim_{x\to a^-}f(x)=-\infty \qquad \lim_{x\to a^+}f(x)=-\infty \qquad \text{resp.} \]

We say a left or right limit is oscillitory divergent if the limit does not exist and is neither positive nor negative infinity.

To say a limit is defined to be \(\pm\infty\) does not say the limit exists, it merely says the way in which it diverges!

For the function plotted, compute each quantity.

ex_LR_lim.jpg

  1. The limit from the left at \(x=3\).
    \(\displaystyle \lim_{x\to 3^-}f(x)=\,\)

    The limit from the left is the height \(f(x)\) approaches as \(x\) approaches \(3\) from the left, i.e. \(x\) is less than \(3\) but getting very close to \(3\).

    \(\displaystyle \lim_{x\to 3^-}f(x)=4\) because the curve on the left goes to height \(4\) as \(x\) goes to \(3\).

  2. The limit from the right at \(x=3\).
    \(\displaystyle \lim_{x\to 3^+}f(x)=\,\)

    The limit from the right is the height \(f(x)\) approaches as \(x\) approaches \(3\) from the right, i.e. \(x\) is greater than \(3\) but getting very close to \(3\).

    \(\displaystyle \lim_{x\to 3^+}f(x)=2\) because the curve on the right goes to height \(2\) as \(x\) goes to \(3\).

  3. The function value at \(x=3\).
    \(\displaystyle f(3)=\,\)

    The value of \(f(x)\) at \(x=3\) is \(f(3)\) if it is defined. In a plot, it is shown as a solid dot.

    \(f(3)=2\) because the solid dot above \(x=3\) is at height \(2\).

For the piecewise function shown, compute each quantity.

\[ f(x)=\left\{ \begin{matrix} x-2 & \text{if} & x\lt4 \\ 2 & \text{if} & x=4 \\ x-1 & \text{if} & x\gt4 \end{matrix}\right. \]

  1. The limit from the left at \(x=4\).
    \(\displaystyle \lim_{x\to 4^-}f(x)=\,\)

    The limit from the left is the value \(f(x)\) approaches as \(x\) approaches \(4\) from the left, i.e. \(x\) is less than \(4\) but getting very close to \(4\). So use the formula for \(x\lt4\).

    \(\displaystyle \lim_{x\to 4^-}f(x)=2\) because to plug in numbers less than \(4\) we use the first formula. So for \(x=3.9,3.99,3.999\) we get \(f(x)=1.9,1.99,1.999\) which approach \(2\).

  2. The limit from the right at \(x=4\).
    \(\displaystyle \lim_{x\to 4^+}f(x)=\,\)

    The limit from the right is the value \(f(x)\) approaches as \(x\) approaches \(4\) from the right, i.e. \(x\) is greater than \(4\) but getting very close to \(4\). So use the formula for \(x\gt4\).

    \(\displaystyle \lim_{x\to 4^+}f(x)=3\) because to plug in numbers greater than \(4\) we use the third formula. So for \(x=4.1,4.01,4.001\) we get \(f(x)=3.1,3.01,3.001\) which approach \(3\).

  3. The function value at \(x=4\).
    \(\displaystyle f(4)=\,\)

    The value of \(f(x)\) at \(x=4\) is the number given next to \(x=4\) if it is defined.

    \(f(4)=2\) because to plug in \(x=4\) we use the second formula.

© MYMathApps

Supported in part by NSF Grant #1123255